Visualizing a Hypersphere
There's lots to be found on the internet on the subject of higher-dimensional spheres. There are all kinds of wonderful sites of any level of mathematical detail that you could care to read. And this one is mine.
Here I attempt to document a particular bit of noodling I did on the subject once. There are diagrams and pictures that should go along with it, which maybe I'll get around to drawing or otherwise creating. In particular, I tried to reconcile to myself two descriptions I'd used/heard in proofs and discussions regarding hyperspheres. One (I think from Ian Stewart's Flatterland) involves picturing successive 3-D slices as spheres of varying color: the fourth dimension runs from blue to red (through purple), and as we shift our slice-plane in one direction, the big purple sphere gets smaller and bluer, and going back the other way it grows back to its full purple size and then keeps getting redder as it shrinks again toward its center.
Work with this one a second. Big purple sphere sitting in the middle of the room. We have our little cage that slides back and forth along the fourth dimension (traditional terms for directions along the fourth dimension include “ana” and “kata”, etc. But I'll probably mostly stick with red and blue in this discussion, since that's easier to picture, and picturing is the whole point of this page). Press one pedal, and we see slices more towards blue, which are of course smaller (as you approach the extremities of any dimension, the sphere gets smaller of course) and bluer, until it's just a little blue dot at the center of what was the big sphere. Press the other pedal, and the blue dot grows and gets redder, becomes the big sphere at midway purple, and then gets smaller but redder. Remember that all the points on all these variously-colored spheres are present at the same time; the sequential presentation is just an illusion caused by looking at them slice by slice. So you can imagine the non-purple points to fill the whole space inside the purple sphere; every 3-dimensional point is the projection of two 4-dimensional points on the hypersphere, one on the blue side and one on the red side—but they're still all on the surface of the hypersphere.
A word on terminology. Although it might seem obvious that we should refer to the four-dimensional sphere as a “4-sphere” and to the three-dimensional one as a “3-sphere”, in fact it isn't that simple. Some mathematicians do use that terminology, but many, especially topologists, whose field is very intimately concerned with these sorts of shapes, have a different modeling. Topologists are concerned mostly with the surfaces of things, as the name implies. Since the surface of a 3-dimensional sphere is a 2-dimensional space (it's like a plane curved around the sphere, you see), the surface of the 3D sphere is called a “2-sphere”, or S2. So too, the surface of a 4D sphere is a “3-sphere” or S3 and so on. The inside of the 3D sphere itself (not its surface) is called a “3-ball” or B3 and so forth. Sn-1 is the surface of Bn. Isn't math fun?
OK. Now for the other view of the hypersphere that I heard. This came from a lecture I heard on an application of the Fixed-Point Theorem, namely the so-called Hairy Ball Theorem. Imagine a fuzzy sphere; each point on the sphere has a little tiny hair growing out of it (these are imaginary, differential hairs, okay? They're simple one-dimensional line segments of arbitrarily short length, coming out of every single point). You need to comb all those hairs flat, in some continuous fashion without abrupt changes of direction. You can't have abrupt changes of direction, since after all there's a hair on every point and there'll be points along the boundary of your change that won't know what to do. If you think about it, you can't do it. You can't comb all the hairs down neatly. You can try going 'round and 'round in circles around the lines of latitude—but then what will happen at the poles? Same problem if you try combing everything toward one pole. This implies, by the way, that there has to somewhere on Earth where the wind isn't blowing. It also means that every reasonably full, freely flowing head of hair has to have a cowlick, where the hair spirals out.
Now try doing the same task with the surface of a 2-dimensional
ball
, i.e. a circle. A fuzzy circle can easily have its hairs all
combed down: just comb them all around it clockwise (or counterclockwise).
As the Mathworld link above will tell you, it turns out this is possible
whenever the number of dimensions is odd, but not when it's even.
(Remember, the ordinary 3-dimensional case counts as even, because
we're dealing with the 2-sphere S2, and the 2D circle is
odd because it's S1. Those wacky
topologists.) So you can comb down the hairs of a fuzzy 4D
hypersphere (which is good to know if you ever get a job as a barber in
four dimensions). And that theorem is what the lecture I attended was
about. The lecturer actually proved the general case, for
all n, and when giving the background and bringing up the 4D
case as an example, he quickly explained it was possible, since after all,
a 4D hypersphere is equivalent to two circles: one in the
east/west × north/south plane, and one in the
up/down × blue/red plane, and you can comb each circle
around like we
said before. And that makes sense, sort of... but how does it jibe with
the multicolored sphere from the other model? Specifically, what do these
two circles look like on the multicolored sphere? That's what I'm trying
to reconcile here.
Well! You've read probably something over a solid page of text (depending on your browser), more than many web pages ever have all together... and you've managed to make it past the introduction, ready to get to the actual description. Is it too late to warn you that I'm long-winded?
So let's consider where these circles are. It isn't just two circles, obviously. It's two families of circles, one of each of which intersect at every point on the hypersphere. That is, through each point on the hypersphere (the surface, remember), passes one horizontal circle and one vertical/chromatic circle (that's what I'm going to call the fourth direction, since I'm representing it by color). Naturally, they don't have to be horizontal and vertical and whatever, presumably they can be any orthogonal directions, but without loss of generality this is how I'm lining them up for the sake of discussion.
The horizontal circles we can imagine easily enough. They go around the sphere like lines of latitude. Each such circle has a fixed vertical position and a fixed color, or to look at it another way, these circles live horizontally, in stacks of growing and shrinking radius, on each of the 3-dimensional spheres of various colors that make up the hypersphere's slices. (Yes, they also stack up chromatically at each fixed vertical position, but we're building up to understanding that; we don't need to work with it yet).
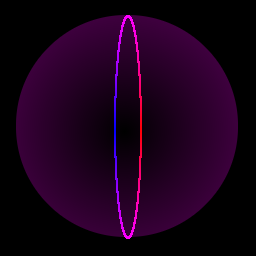
What about the vertical/chromatic circles? Each one lives along a vertical line segment inside the large purple 3D sphere, when looked at in only 3 dimensions. It starts at the top, at the intersection of the largest 3d sphere (which we should probably call a Great Sphere, like a great circle is a slice of a sphere which contains its center) with the vertical line we're looking at. That is in perfect midpoint purple, then proceeds vertically downward, into the sphere (it looks that way, of course, but it's still on the outside of the hypersphere) becoming redder and redder until it reaches its reddest point just where it crosses the vertical midline. There's a picture to the right; I've artificially expanded the circle to make it a narrow ellipse in the two dimensions I'm drawing, but really it's a one-dimensional vertical line if you don't count the color dimension. So its color changes fastest at the top and at the bottom, where it's perfectly purple—that is, when it crosses the midplane of the chromatic axis (which is at the extrema of its vertical movement), it is at a high angle, in fact it is perpendicular to the plane at that point. The color-change is the slowest when it reverses direction, at its red and blue extremes. Note that it won't get fully red or blue (i.e. as red/blue as the hypersphere gets) except at the great circle which goes through the center of the sphere. That's all perfectly okay and sensible. Note that we don't have to think about what the circles do in the “other” spheres, the redder and bluer ones. The circles span the chromatic dimension, there's only one circle for each point in the horizontal plane, passing through all the points on the sphere with those horizontal coordinates, no matter the vertical or chromatic coordinates.
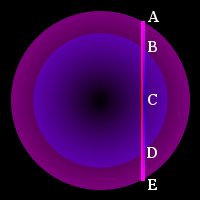
Let's make sure we have these pictured; this is the hardest part. Take a look at the picture to the left. In order to get away from special cases, we are looking at an “off-center” circle, one that doesn't pass through the center of the sphere. That circle is represented by the vertical line in the picture. Recall that the 3D projection of the circle is just a vertical line segment. The topmost extent is at point A, which is where the circle in question intersects with the “Great Sphere”, the big purple one. From there, the circle descends vertically, going downward and blue-ward (shown here on the right side of the vertical line). I've drawn another sphere in for reference. It's one of the smaller spheres on the blue side of purple. When the circle gets to the right shade of blue, it is at point B, where it intersects with the smaller circle, at the same height and the same blueness. There are lots of other spheres it does the same thing with; I'm just showing one as an example. The point we're imagining going around the circle is sliding downward and blue-ward, always riding on the surface of the hypersphere, always riding on the surface of the appropriately-colored 3d sphere. It reaches its maximum blueness at point C, where it crosses the midline. Note that its maximum blueness is not the same as the bluest extent of the sphere! The sphere reaches its very most blue, its blue pole, at the center of the Great Sphere (in 3D; obviously it's farther away in the blue direction). The bluest our circle gets is the color of the smallest blue sphere that touches that line, the sphere which would be tangent to it if it were just a line. After point C, it reverses chromatic direction and starts getting redder as it goes downward. At the right shade, it again touches our bluish sphere, at point D, still becoming redder (and getting faster at getting redder) until it reaches perfect midpoint purple at point E, its lowest vertical point. There, it reverses vertical direction—but not chromatic direction—and heads back upward, still getting redder, now on the red side of purple (I'm showing that here on the left side of the line). Back at point D, it now does not intersect the bluish sphere, because it's now on the redder side, so it's passing through an identically-sized reddish sphere. It reaches maximum redness back at point C, where it was also maximally blue. Note that the circle never actually intersects or touches itself (how can it? Circles can't intersect themselves and remain circles). It seems to occupy the same point twice when projected into three dimensions, but each time it's a different color, i.e. at a different location in the chromatic direction. From point C again, it continues on up, getting bluer now as it's reached maximum redness, getting to point B when it's as red as it was blue when it passed through it the first time. (Read that again, it makes sense.) Eventually it gets red enough to be at midpoint purple again, just where we started back at point A. Whew. Did that help?
And the hairs on those circles? That's what we need to look at. Once we have those, we can say we're done, because the hair-combing on the hypersphere as a whole will be the vector sum of the horizontal hair and the vertical/chromatic hair that come from each point. The hairs on these circles, of course, point in a combination of up/down and red/blue directions. Imagine a particle sliding along the circle; its direction at any instant is where the hair points. Note that just where the up/down motion is slowest, at the top and bottom where it changes over from going up to down and vice-versa, the red/blue motion is the fastest (see the above diagram again). At those points, it's speeding steadily from red to blue (or the other way). Conversely, when it's at its extrema of red/blue, turning around to go the other direction at the vertical midpoint, the vertical motion is fastest. So we can see how the hairs comb around it.
OK! Now at each point we have a hair in the horizontal direction (from the horizontal circle passing through the point) and a hair in the vertical/chromatic direction (from the vertical/chromatic circle). We can add those together as a vector sum to get one combined hair. But lengths don't really matter, and the two hairs are at right angles to each other, so the direction of the “combined hair” is just the direction of the angle bisector of the angle between the two hairs. Yes, it makes sense to talk of an angle here. One hair is pointing, say, at a slope of 3 units east per 2 units north (i.e. measuring the angle from the eastern axis, tan θ=2/3). The other is point, for the sake of argument, at a slope of 1 unit upward per 2 units blue-ward, so tan φ=2, measuring angles from the upward axis). Add those two angles together. Imagine taking something pointing at angle θ in the horizontal plane and rotating it up-and-blueward by φ. It doesn't matter if you can't really mentally do the math, so long as you can conceive that it's possible to do that, and thus combine the two combings into one continuous combing of fuzz all around the hypersphere.
Just to stick a fork in this thing for good, let's take a look at some edge cases. If anything is going to go wrong, we'd expect it to happen at the poles, right? Where the ends of the axes poke through the hypersphere. That's where it fell apart for us when we tried our tonsorial talents on the 3d sphere: we could comb around, but the top and bottom poles were the problem. So, let's look at the ends of the axes. There are eight of them, but without loss of generality we'll just look at the positive halves, so that's only four. Two of those are pretty simple. The east and north axes poke out of the hypersphere on the Great Sphere (the purple one) along its equator around its middle. Argh, terminology is confusing things again. North and East refer to the room that the sphere is in, not to directions on the sphere like on a globe. Keep that in mind. OK, so those poles are on the equator of the purple sphere. At those points, the hairs are pointing straight sideways, across the axis (i.e. at the east pole, the hair points due north or south, depending on how you combed the hairs: the north/south dimension doesn't contribute, and neither do the other two). The hair doesn't really point up or down or blue or red at those points, because we're at the limiting cases for those. A little way in from the pole, we have teeny tiny circles that get smaller and smaller until we get to the pole. The extent of the hypersphere in the vertical and chromatic direction vanishes at the pole, so it makes no contribution. Those contributions were getting smaller and smaller as we approached the pole anyway, so it's continuous.
Now let's see the upward pole, the very top of the sphere. Here we have the opposite situation: the two horizontal contributions go to zero because the circle gets vanishingly small, and the vertical contribution is also zero because this is just where that vertical circle is switching over from going up to going down, so it's not pointing up or down either. But it's at its maximum in the chromatic direction: there's a hair pointing due red (or blue). And don't forget to look at the blue pole. That's located in the center of the sphere in 3-space, but all the way on the blue end. The horizontal contributions are still zero, because the sphere has become minimally small and it doesn't have extent in those directions. Its chromatic direction is also zero because the circle that passes through here is just switching over from heading blue-ward to heading red-ward. Remember, this is the blue-most peak of the hypersphere. But the vertical contribution is at its strongest. Travelling in the vertical direction, this is right where the sphere is about to explode outward as fast as it ever does (or it's just finished exploding inward, depending on how you look at it). There's a hair there pointing straight up (or down), and all other contributions approach zero as we approach that point.
Whew. Well, I think we've taken this about as far as we can for now, and if you really ponder it more, the hypersphere starts making more sense. You can start to imagine, for example, skew circles, that don't lie in any plane parallel to the axes, so they have extents in all four dimensions. Maybe work on how a torus looks painted on the surface looks (I think there's an xscreensaver mode called hypertorus that shows a torus on a rotating hypersphere. See if you can make sense out of what it shows). Did this site help you at all? Let me know.